I discovered Fibonacci today. I have to admit that I was flabbergasted at the discovery.
For some period of time, when I groaned about loosing a particular game of chess, my son often suggested it was because I used "
The Fibonacci". Thinking the word was my son's made up slang word, it seemed applicable to winning or losing chess games so I added it to my vocabulary and blame many of my losses on "
Fibonacci".
You can imagine my astonishment when I came across the word Fibonacci while surfing the Internet. I googled for it and voilà!
In mathematics
Fibonacci numbers or Fibonacci sequence are numbers in the following integer sequence, 0,1,1,2,3,5,8,13,21,34,55,89,144
The first two numbers in the Fibonacci sequence is 0 and 1, (alternatively, 1and1). Each subsequent number is the sum of the previous two. 1+1=2, 1+2=3, 2+3=5 etc.
The sequence is named after
Leonardo of Pisa, known as Fibonacci.
In my art studies, I learned about the
Golden Ratio or golden mean which is believed to be the most pleasing and beautiful shape. It is found in many places including geometry, art and architecture such as the Parthenon. Using 'rule of thirds' divide a line into two parts so that the longer part divided by the smaller part
is also equal to the whole length divided by the longer part you will have the golden ratio.
 |
| Golden Ratio |
What does this have to do with Fibonacci numbers? I never knew about them and their special relationship to the golden ratio.
The symbol of golden ratio uses the Greek letter '
phi'

which is a special number equal to 1.618. The ratio of any two successive numbers is close to the golden ratio.
Fibonacci sequence numbers appear in nature and biological settings such as branches of trees, leaf and petal placement such as pine cones, pineapples, broccoli florets and sunflower seeds which arrange themselves in spirals.
Until recently it was believed the beautiful chambered nautilus was an example of golden ratio, but recent scientific study shows the spiral of the nautilus doesn't have the true spiral shape based on the golden ratio.
The following shows how
Fibonacci numbers look if tiled in squares and in spirals.
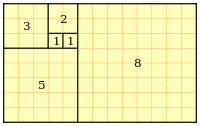 |
| Fibonacci numbers tiled in squares |
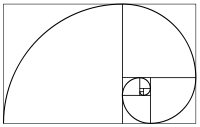 |
| Fibonacci numbers tiled in spirals |
The tiling is made of squares whose sides are successive Fibonacci numbers in length.
A spiral is created by circular arcs connecting to opposite corners of squares.
What a delight to find new information to add to what I already knew. And to top it off, I can now use the word 'fibonacci' as having two meanings, my own personal slang word and one mathematical.












